11. 데이터베이스 설계 이론
- 나쁜 스키마에는 3가지 이상(anormaly)이 있음.
1) 갱신 이상
2) 삭제 이상
3) 입력 이상
course 테이블과 department 테이블을 합쳐서 다음과 같은 테이블을 만듦.
->mybadtable1(cID, title, deptName, credit, chairman, building, budget)
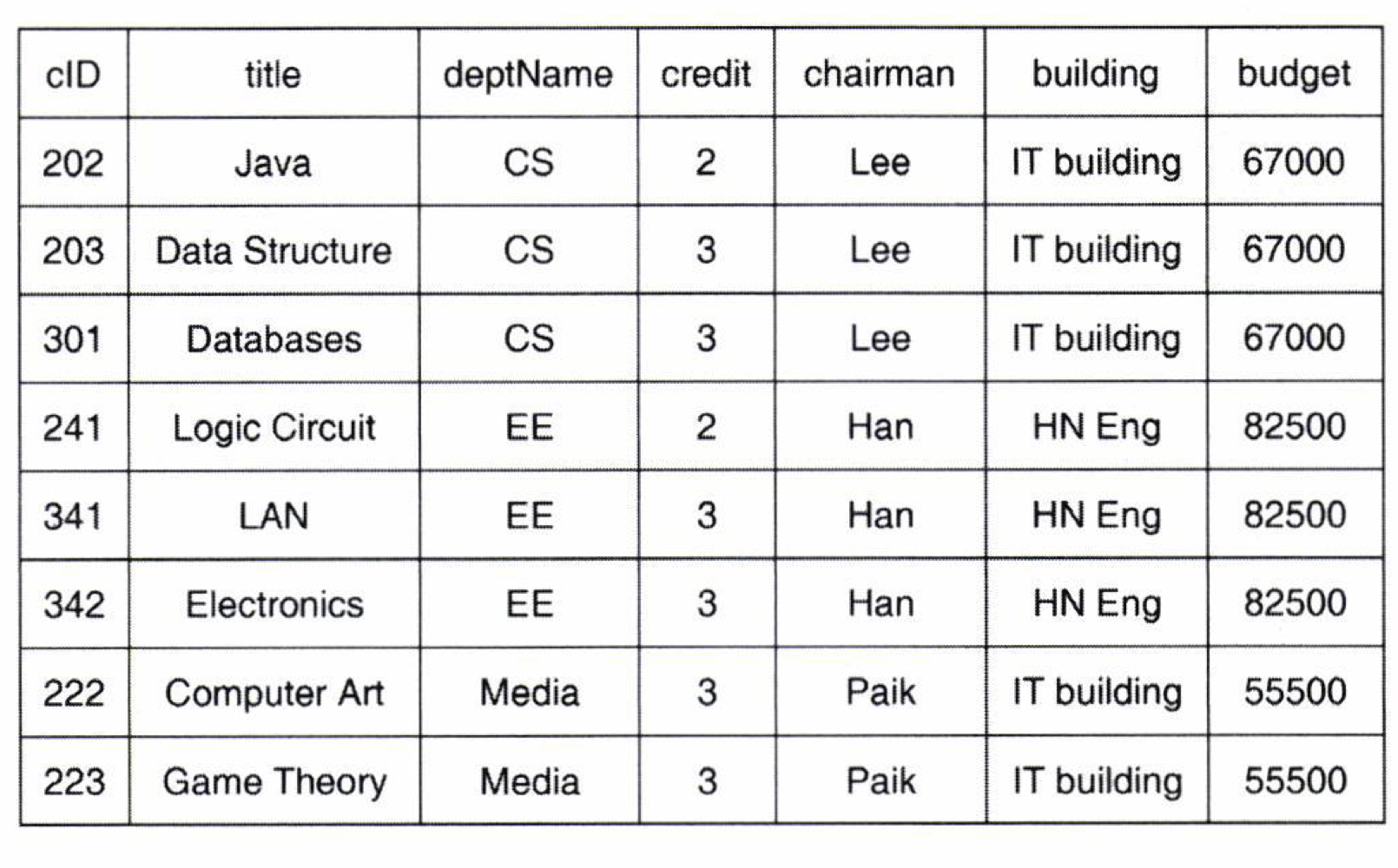
이 테이블은 나쁜 스키마인데...
- Update anormaly 측면
chairman을 하나만 바꿔도 여러개 다른 row들에서도 바꿔줘야 함. ->redundancy(중복성) 유지 X
- Delete anormaly 측면
만약 Java, Data, Structure, Databases 모두 사라지면 CS과에 대한 정보들도 같이 삭제됨.
-Insert anormaly 측면
새로운 과를 신설해두려고 함. 하지만 해당 과에 과목을 지정을 같이 하지 않으면 신설 불가능.(∵cID가 PK이기 때문)
- Functional Dependency(함수 종속성)
: 유효한 관계 인스턴스에 대한 제약으로 일부 속성 값이 다른 속성 값을 유일하게 결정함을 의미함.

- 슈퍼키 : 관계 속성의 일부분으로서 전체 속성을 함수적으로 결정하는 속성
- 후보키 : 슈퍼키의 성질을 만족하면서 슈퍼키의 성질을 만족하는 서브셋이 없는 속성 셋.
- 함수 종속성의 사용
1) 주어진 관계 인스턴스의 유효성을 검사
2) 적법한 테이블의 제약 조건을 명시
- trivial(무의미한) 함수 종속성
: 함수 종속성이 테이블의 모든 인스턴스에 대하여 만족이 되는 경우
- 함수 종속성의 폐포(closure)
: 주어진 함수 종속성 집합으로부터 유추할 수 있는 모든 함수 종속성을 가진 집합
- 암스트롱 공리(Armstring Axioms)
: 새로운 함수 종속성을 유추할 수 있는 추론 규칙

1) 재귀성(reflexivity) : 무의미한 함수 종속성을 생성함.
2) 부가성(augmentation) : 주어진 함수 종속성에 동일한 속성을 양쪽에 추가하여도 됨.
3) 이행성(transivity) : 추론의 이행성을 설명하는 것.
이 규칙들은 1) sound(새롭게 생성되는 규칙이 유효함) 2) complete(모든 유효한 함수 종속성을 암스트롱 공리를 이용하여 생성할 수 있음 ) 해야 한다.
+추가 규칙
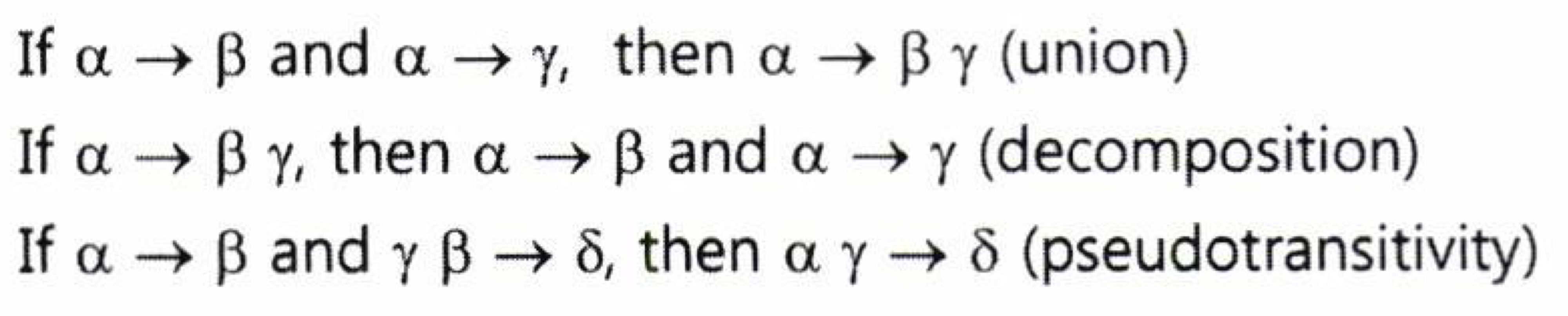
- 위 규칙들을 가지고 쭉쭉 해나가면 Closure를 구할 수 있음.
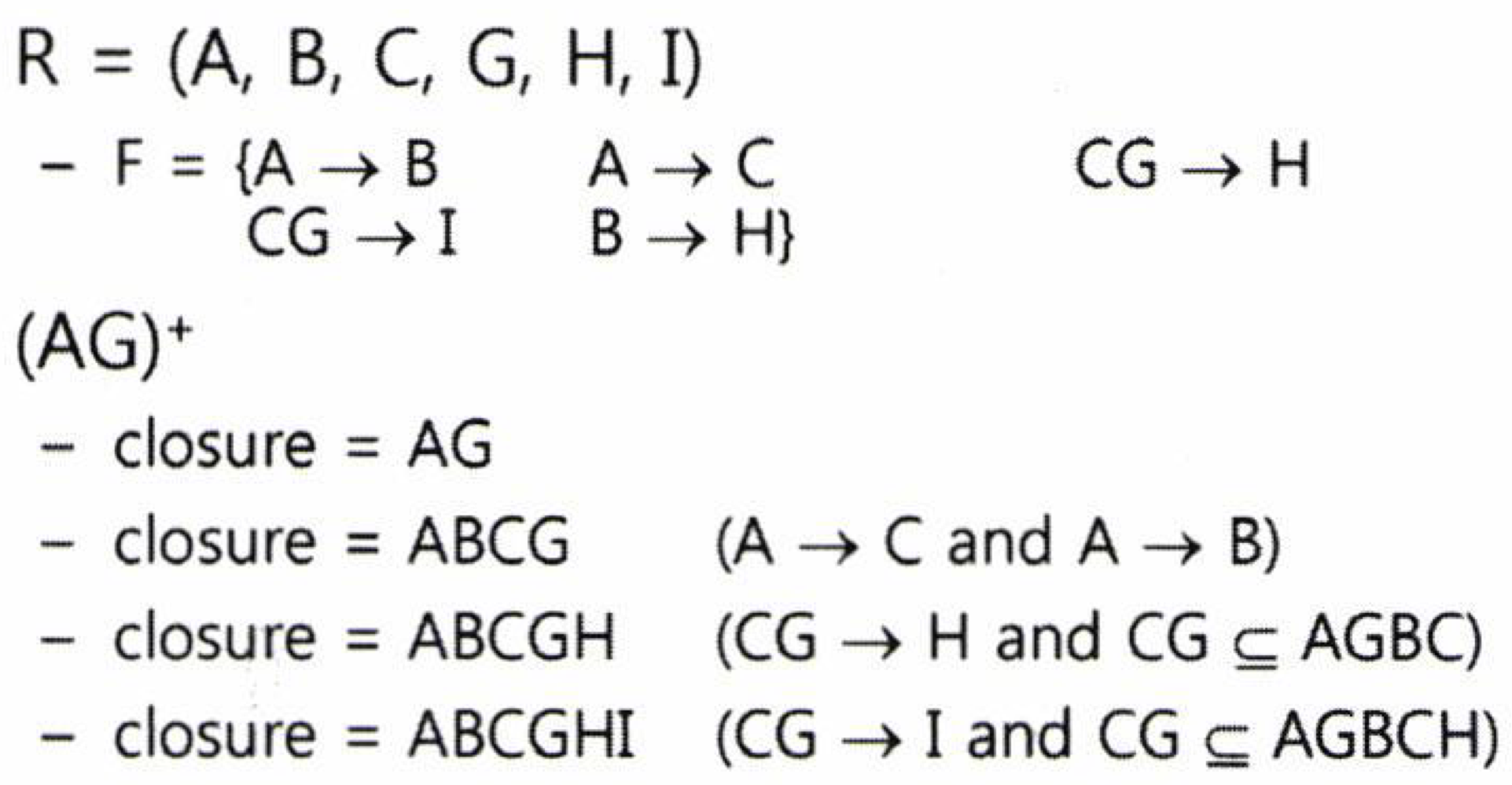
- 속성 폐포의 사용
1) 주어진 속성이 슈퍼 키인지 검증할 때 사용
2) 주어진 함수 종속성이 유효한지 검증(a->b에 대해 a의 closure에 b가 속하면 유효한 FD임)
- 정규 커버(=최소 커버, Canonical cover)
redundant한 FD를 제거한 FD set

- 정규형
제 1~3정규형, BCNF는 함수 종속성을 이용하여 정의
제 4정규형은 다치 종속성을 이용하여 정의
- 제 1정규형
: 도메인의 모든 값이 원자 값인 정규형
- 주요 속성 / 비주요 속성
: 다수 개의 후보 키가 존재할 때 최소 하나 후보 키에 속하면 주요 속성임.
- 완전 함수 종속성
: a->b에서 a의 어떤 부분집합 r도 r-> b를 만족하지 않는 경우
만약 이를 만족하면 '부분 함수 종속성'이라고 함.
- 이행 함수 종속성
: a->b, b->r 일 때 a->r을 뜻함.
- 제 2정규형
: 모든 비주요 속성이 모든 후보 키에 완전 의존적인 정규형

- 제 3정규형
: 제 2정규형 중에서 비주요 속성이 모든 후보 키에 이행적으로 의존적이 아닌 정규형
혹은
모든 의미 있는 함수 종속성 a->b에서 a가 슈퍼 키이거나 또는 b가 주요 속성인 정규형

- BCNF
: 관계형 스키마가 모든 의미 있는 함수 종속성 a->b에서 a가 슈퍼 키인 정규형

※ 속성이 2개인 테이블은 무조건 BCNF!!!!!!!